Κεφ. 56ο: Διαιρέσεις (ΙΙ) - Μαθηματικά Γ' Δημοτικού

Στο πεντηκοστό έκτο κεφάλαιο των μαθηματικών της Γ' Δημοτικού, θα μάθουμε να εφαρμόζουμε την πράξη της διαίρεσης σε καθημερινές καταστάσεις, όπου η διαίρεση εμφανίζεται με τη μορφή μερισμού ή μέτρησης. Ειδικότερα, θα μάθουμε να εκτελούμε κάθετες (με δύο κάθετες γραμμές) διαιρέσεις, τον γραπτό αλγόριθμο της διαίρεσης, καθώς και να αντιστοιχίζουμε το πηλίκο και το υπόλοιπο, στους κατάλληλους αριθμούς μιας διαίρεσης.

Πάμε να δούμε ποιες εργασίες και ασκήσεις έχει το βιβλίο μαθητή και το τετράδιο εργασιών, και πώς θα τις λύσουμε.

1. Τα βιβλία. 5 μαθητές κατέβασαν από τη βιβλιοθήκη 42 βιβλία. Θέλουν να τα μοιραστούν μεταξύ τους. Πόσα βιβλία θα πάρει ο καθένας;

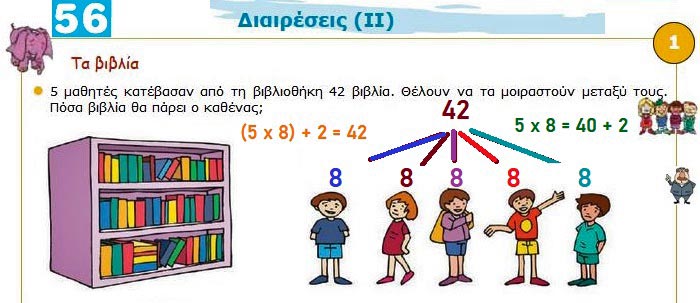
Υπολογίζω και συμπληρώνω τις πράξεις
5 x 8 = 40
42 = (5 x 8) + 2

Η Κορίνα γράφει αυτή την πράξη με έναν διαφορετικό τρόπο.
👉 Η Κορίνα για να μπορέσει να κάνει (πιο εύκολα) αυτή την πράξη, τη διαίρεση, χρησιμοποιεί μια μέθοδο, που λέγεται κάθετη διαίρεση. Στη μέθοδο αυτή, για να υπολογίσουμε το αποτέλεσμα (πηλίκο), τραβάμε δυο κάθετες (μεταξύ τους) γραμμές και μετά τοποθετούμε τους αριθμούς που θέλουμε να διαιρέσουμε (Διαιρετέο και διαιρέτη) με συγκεκριμένο τρόπο. Πρώτα γράφουμε αριστερά από την κάθετη γραμμή τον αριθμό που θέλουμε να διαιρέσουμε (Διαιρετέο) και μετά, δεξιά από τη γραμμή, τον διαιρέτη (αυτόν που μας λέει σε πόσα ίσα μέρη θα χωρίσουμε-μοιράσουμε το Διαιρετέο).
Η Κορίνα λοιπόν γράφει το 42 στη θέση του Διαιρετέου και το 5 στη θέση του διαιρέτη. Έπειτα σκέφτεται πόσες φορές «χωράει» το 5 στο 48 και βρίσκει 8, γιατί 5 επί 8 κάνει 40 (που χωράει στο 42), ενώ 5 επί 9 κάνει 45 (που δεν χωράει στο 42, αφού είναι μεγαλύτερο) οπότε γράφει το 8 κάτω από το διαιρέτη. Ακολούθως λέει: 5 x 8 = 40 από 42 κάνει 2, οπότε το γράφει εκεί που γράφουμε το υπόλοιπο, δηλαδή κάτω από το Διαιρετέο.
► Έτσι βρήκε ότι κάθε παιδί θα πάρει από 8 βιβλία και θα περισσέψουν 2.

• Τα παιδιά θέλουν να τοποθετήσουν 42 βιβλία σε 6 κουτιά. Πόσα βιβλία θα βάλουν σε κάθε κουτί;
6 x 7 = 42
42 = (6 x 7) + 0

👉 Με τη μέθοδο της Κορίνας γράφουμε:
Το 42 αριστερά στη θέση του Διαιρετέου και το 6 δεξιά στη θέση του διαιρέτη.
Μετά λέμε: Το 6 χωράει 7 φορές στο 42, το γράφουμε και λέμε, 6 x 7 = 42 από 42 ίσον 0 και το γράφουμε.
► Άρα τα παιδιά θα βάλουν σε κάθε κουτί 7 βιβλία.

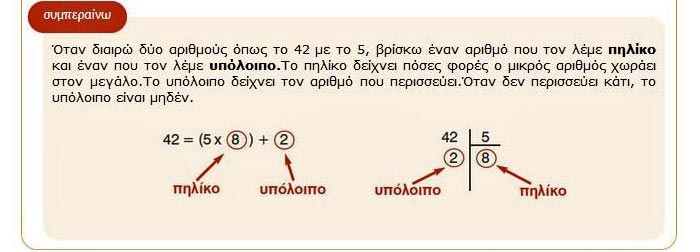
Συμπεραίνω 👉 Όταν διαιρώ δύο αριθμούς όπως το 42 (διαιρετέος) με το 5 (διαιρέτης), βρίσκω έναν αριθμό (το 8), που τον λέμε πηλίκο και έναν (το 2), που τον λέμε υπόλοιπο.
👉 42 = (5 x 8) + 2
Το πηλίκο δείχνει πόσες φορές ο μικρός αριθμός χωράει στον μεγάλο.
Το υπόλοιπο (2) δείχνει τον αριθμό που περισσεύει.
Όταν δεν περισσεύει κάτι, το υπόλοιπο είναι μηδέν.

2. Κάνω τις διαιρέσεις και γράφω το αποτέλεσμα.
► 48 : 6 = 8 | 63 : 7 = 9 | 56 : 8 = 7 | 64 : 8 = 8 | 63 : 9 = 7 | 72 : 9 = 8

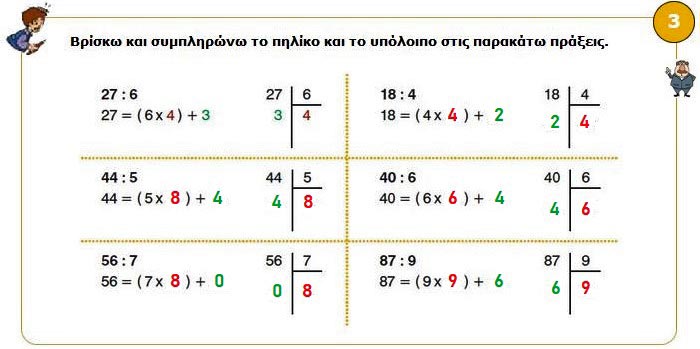
3. Βρίσκω και συμπληρώνω το πηλίκο και το υπόλοιπο στις παρακάτω πράξεις.
27 : 6                  |  18 : 4
27 = (6 x 4) + 3        |  18 = (4 x 4) + 2

44 : 5                  |  40 : 6
44 = (5 x 8) + 4        |  40 = (6 x 6) + 4

56 : 7                  |  87 : 9
56 = (7 x 8) + 0        |  87 = (9 x 9) + 6

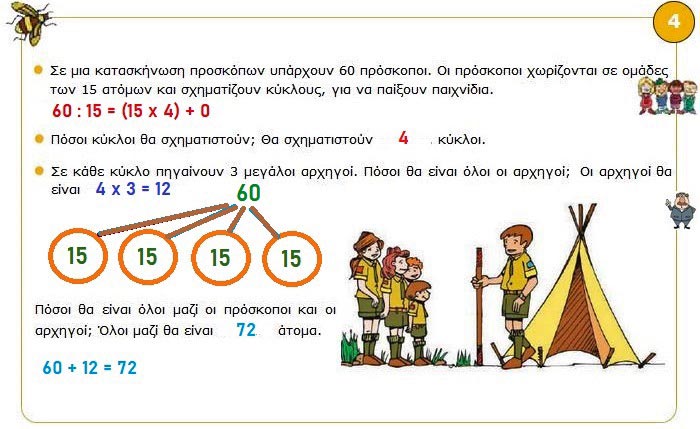
4. Σε μια κατασκήνωση προσκόπων υπάρχουν 60 πρόσκοποι. Οι πρόσκοποι χωρίζονται σε ομάδες των 15 ατόμων και σχηματίζουν κύκλους, για να παίξουν παιχνίδια. Πόσοι κύκλοι θα σχηματιστούν; Θα σχηματιστούν: 60 = (15 x 4) + 0, άρα: 60 : 15 = 4 κύκλοι.

• Σε κάθε κύκλο πηγαίνουν 3 μεγάλοι αρχηγοί. Πόσοι θα είναι όλοι οι αρχηγοί;
Οι αρχηγοί θα είναι: 4 x 3 = 12

Πόσοι θα είναι όλοι μαζί οι πρόσκοποι και οι αρχηγοί;
Όλοι μαζί θα είναι 60 + 12 = 72 άτομα.

Κεφ. 56ο: Διαιρέσεις (ΙΙ) - Τετράδιο Εργασιών - Λύσεις Ασκήσεων

1. Υπολογίζω το πηλίκο και το υπόλοιπο.
► 28 : 5 = (5 x 5) + 3 | 18 : 4 = (4 x 4) + 2  |  27 : 8 = (8 x 3) + 3  |  34 : 6 = (6 x 5) + 4  |  42 : 7 =  (7 x 6) + 0  |  57 : 8 = (8 x 7) + 1

2. Σε μια βιβλιοθήκη υπάρχουν 13 ράφια καθένα από τα οποία περιέχει 18 βιβλία. Σε μια μετακόμιση τοποθετούνται τα βιβλία σε χαρτοκιβώτια των 21 βιβλίων. Πόσα χαρτοκιβώτια θα χρειαστούν;
► Πρώτα θα βρούμε πόσα είναι συνολικά τα βιβλία: 13 x 18 = 234.
Έπειτα θα τοποθετήσουμε τα 234 βιβλία σε κιβώτια που χωράνε 21. Για να βρούμε πόσα κιβώτια θα χρειαστούμε θα κάνουμε διαίρεση, δηλαδή θα διαιρέσουμε το 234 : 21 = (21 x 11) + 3, άρα θα χρειαστούμε 11 + 1 = 12 κιβώτια.

• 6 χαρτοκιβώτια περιέχουν 300 καινούργια βιβλία. Πόσα βιβλία περιέχει κάθε χαρτοκιβώτιο;
► Ξέρουμε πόσα βιβλία έχουν τα πολλά (6) κιβώτια και θέλουμε να βρούμε πόσα έχει το ένα, οπότε θα κάνουμε διαίρεση: 300 : 6 = (6 x 50) + 0, άρα 300 : 6 = 50 βιβλία.

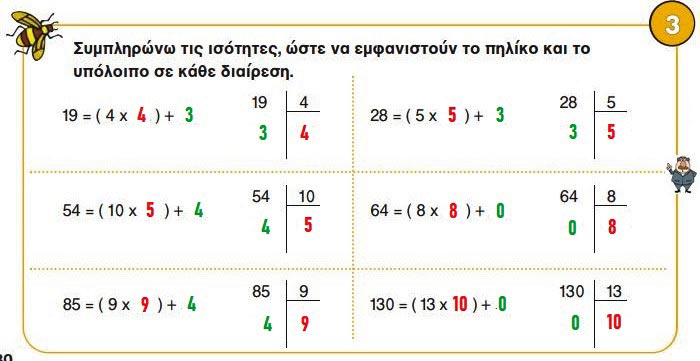
3. Συμπληρώνω τις ισότητες, ώστε να εμφανιστούν το πηλίκο και το υπόλοιπο σε κάθε διαίρεση.
19 = (4 x 3) + 3  |  28 = (5 x 5 ) + 3
54 = (10 x 5) + 4  |  64 = (8 x 8) + 0
85 = (9 x 9) + 4  |  130 = (13 x 10) + 0

4. Κάνω τις διαιρέσεις και γράφω το αποτέλεσμα.
►  48 : 12 = 4 γιατί 48 : 12 = (12 x 4) + 0
►  60 : 12 = 5 γιατί 60 : 12 = (12 x 5) + 0
►  72 : 12 = 6 γιατί 72 : 12 = (12 x 6) + 0
►  88 : 11 = 8 γιατί 88 : 11 = (11 x 8) + 0
► 228 : 12 = 19 γιατί 228 : 12 = (12 x 19) + 0
► 143 : 11 = 13 γιατί 143 : 11 = (11 x 13) + 0

5. Γράφω την εκφώνηση ενός προβλήματος, του οποίου η λύση αντιστοιχεί στην παρακάτω ισότητα. (5 x 8) + 4 = 44
► Η γιαγιά Ελένη είχε 44 κέρματα του 1€ και τα μοίρασε εξίσου στα 5 εγγόνια της. Πόσα ευρώ πήρε το κάθε παιδί και πόσα περίσσεψαν;

Δίνω το πρόβλημα να το λύσει ο διπλανός μου.
► 44 : 5 = (5 x 8) + 4, άρα κάθε παιδί πήρε από 8€ και περίσσεψαν 4€.

6. Υπολογίζω και συμπληρώνω το πηλίκο και το υπόλοιπο στις παρακάτω διαιρέσεις.
► 20 : 6  = (6 x 3) + 2  |  34 : 5 = (5 x 6) + 4  |  80 : 8 = (8 x 10) + 0

► 60 : 20 = (20 x 3) + 0  |  48 : 15 = (15 x 3) + 3  |  99 : 11 = (11 x 9) + 0