Κεφ. 30ο: Ο αλγόριθμος του πολλαπλασιασμού - Μαθηματικά Γ' Δημοτικού

Στο τριακοστό κεφάλαιο των μαθηματικών της Γ' Δημοτικού, θα μάθουμε τον αλγόριθμο τού γραπτού πολλαπλασιασμού που χρησιμοποιούμε σήμερα, και πώς να τον αντιπαραβάλουμε με τον πίνακα του πολλαπλασιασμού, που μάθαμε να χρησιμοποιούμε στα προηγούμενα κεφάλαια. Επίσης να ερμηνεύουμε τα επιμέρους γινόμενα του αλγορίθμου που προκύπτουν από τον πολλαπλασιασμό κάθε ψηφίου του πολλαπλασιαστή επί τον πολλαπλασιαστέο με βάση τον πίνακα του πολλαπλασιασμού και να τα θεωρούμε σαν μια πιο σύντομη έκφραση των γινομένων του πίνακα του πολλαπλασιασμού.

Πάμε να δούμε ποιες εργασίες και ασκήσεις έχει το βιβλίο μαθητή και το τετράδιο εργασιών, και πώς θα τις λύσουμε. 

Ο Αλγόριθμος του (κάθετου) πολλαπλασιασμού, είναι μια σειρά συγκεκριμένων βημάτων (πράξεων), που εκτελούνται διαδοχικά, προκειμένου να υπολογίσουμε γρήγορα και εύκολα το γινόμενο δύο αριθμών (παραγόντων).

1. Ο Πυθαγόρας, για να καταλάβει αυτή την τεχνική, συμπληρώνει τις παρακάτω πράξεις και τους αντίστοιχους πίνακες του πολλαπλασιασμού.

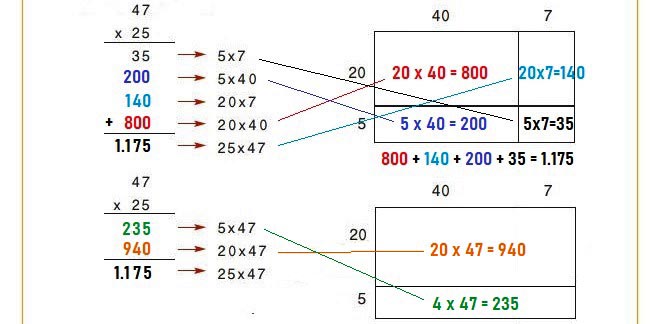
☛ 1ο τρόπος: 25 x 47 = 35 + 200 + 140 + 800 = 1.175
[25 x 47 = (20 + 5) x (40 + 7) = (5 x 7) + (5 x 40) + (20 x 7) + (20 x 40) = 35 + 200 + 140 + 800 = 1.175]

☛ 20 x 40 = 800  |  20 x 7 = 140
☛  5 x 40 = 200  |   5 x 7 = 35

☛ 2ο τρόπος: 25 x 47 = 235 + 940 = 1.175
[25 x 47 = (20 + 5) x 47 = (5 x 47) + (20 x 47) = 235 + 940 = 1.175]

• Χρησιμοποιώ την ίδια τεχνική, για να υπολογίσω το γινόμενο 47 x 32.

☛ 1ο τρόπος: 32 x 47 = 14 + 80 + 210 + 1.200 = 1.504
[32 x 47 = (30 + 2) x (40 + 7) = (2 x 7) + (2 x 40) + (30 x 7) + (30 x 40) = 14 + 80 + 210 + 1.200 = 1.504]

☛ 30 x 40 = 1.200  |  30 x 7 = 210
☛  2 x 40 = 80  |   2 x 7 = 14

☛ 2ο τρόπος: 32 x 47 = 94 + 1.410 = 1.504
[32 x 47 = (30 + 2) x 47 = (2 x 47) + (30 x 47) = 94 + 1.410 = 1.504]

2. Υπολογίζω και γράφω τα γινόμενα.
☛ 18 x 9 = 162,  23 x 3 = 69, 35 x 4 = 140, 44 x 6 = 264, 57 x 3 = 171, 62 x 5 = 310.

3. Γράφω κάθετα και υπολογίζω τους πολλαπλασιασμούς που αντιστοιχούν στους παρακάτω πίνακες.
☛ 15 x 24 = 240 + 120 = 360
☛ 20 x 24 = 240  |  5 x 24 = 120

☛ 36 x 54 = 1.500 + 120 + 300 + 24 = 1.944
☛ 30 x 50 = 1.500  | 30 x 4 = 120
☛  6 x 50 = 300  | 6 x 4 = 24

4. Για να κάνουμε κάθετο πολλαπλασιασμό, τοποθετούμε τους δυο αριθμούς (παράγοντες) τον ένα κάτω από τον άλλο (δεν παίζει ρόλο ποιoν θα βάλουμε πάνω ή κάτω), φροντίζοντας οι μονάδες του ενός, να πάνε ακριβώς κάτω από τις μονάδες του άλλου, οι δεκάδες κάτω από τις δεκάδες κ.λπ.
Έπειτα τραβάμε μια οριζόντια γραμμή και βάζουμε αριστερά από τον πολλαπλασιαστή το σύμβολο του πολλαπλασιασμού, το "X".

Ας δούμε πώς το κάνουμε, χρησιμοποιώντας για παράδειγμα τον πολλαπλασιασμό 67 x 34, που έχει το βιβλίο στην άσκηση 4.

Ξεκινάμε πάντα πολλαπλασιάζοντας τις μονάδες του κάτω αριθμού (που λέγεται πολλαπλασιαστής), με τις μονάδες του επάνω αριθμού (λέγεται πολλαπλασιαστέος) και λέμε: 4 x 7 = 28.
Γράφουμε το 8 κάτω από τις μονάδες και έχουμε 2 ως κρατούμενα.
Μετά πολλαπλασιάζουμε το 4 επί το 6 (τις δεκάδες) και λέμε: 4 x 6 = 24.
Οπότε, 24 και 2 τα κρατούμενα 26. Γράφουμε το 26, με το 6 κάτω από το 3, στη στήλη με τις δεκάδες.

Συνεχίζουμε με τις δεκάδες του πολλαπλασιαστή και τις πολλαπλασιάζουμε με τις μονάδες του πολλαπλασιαστέου, δηλαδή: 3 x 7 = 21. Γράφουμε το 1 κάτω από τις δεκάδες και έχουμε 2 κρατούμενα.

Μετά πολλαπλασιάζουμε τις δεκάδες επί τις δεκάδες, δηλαδή: 3 x 6 = 18.
Και λέμε, 18 και 2 τα κρατούμενα που έχουμε κάνει 20. Το γράφουμε με το 0 κάτω από τις εκατοντάδες.

Τέλος τραβάμε γραμμή, βάζουμε το σύμβολο της πρόσθεσης, το "+", και προσθέτουμε τα δύο μερικά γινόμενα, το 268 με 2010.
Το αποτέλεσμα της πρόσθεσης που βρήκαμε, το 2.278, είναι το γινόμενο του πολλαπλασιασμού που κάναμε.

 Κεφ. 30ο: Ο αλγόριθμος του πολλαπλασιασμού - Τετράδιο Εργασιών - Λύσεις Ασκήσεων

1. Υπολογίζω και γράφω τα γινόμενα.
☛ 14 x 20 = 280, 21 x 30 = 630, 34 x 20 = 680, 18 x 30 = 540, 12 x 40 = 480, 15 x 50 = 750.

2. Εκτελώ τους παρακάτω πολλαπλασιασμούς.
☛ 25 x 43 = (20 + 5) x 43 = (5 x 43) + (20 x 43) = 215 + 860 = 1.075
☛ 46 x 52 = (40 + 6) x 52 = (6 x 52) + (40 x 52) = 312 + 2.080 = 2.392
☛ 53 x 64 = (50 + 3) x 64 = (3 x 64) + (50 x 64) = 192 + 3.200 = 3.392
☛ 30 x 75 = (30 + 0) x 75 = (30 x 75) = 2.250
* Στην τελευταία πράξη δεν πολλαπλασιάζουμε το 0, αφού με όποιο αριθμό και να το πολλαπλασιάσουμε κάνει μηδέν και δεν αλλάζει το αποτέλεσμα, απλά το γράφουνε στη θέση των μονάδων.

3. Συμπληρώνω τα γινόμενα με βάση την πράξη του πολλαπλασιασμού και φτιάχνω τον αντίστοιχο πίνακα του πολλαπλασιασμού.
☛ 54 x 73 = (50 + 4) x 73 = (4 x 73) + (50 x 73) = 292 + 3.650 = 3.942
☛ 50 x 73 = 3.650  |  4 x 73 = 292
  292 + 3.650 = 3.942

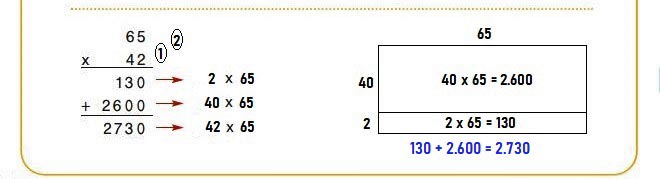
☛ 42 x 65 = (40 + 2) x 65 = (2 x 65) + (40 x 65) = 130 + 2.600 = 2.730
☛ 40 x 65 = 2.600  |  2 x 65 = 130
  130 + 2.600 = 2.730

4. Υπολογίζω και γράφω τα γινόμενα.
☛ 40 x 10 = 400, 20 x 20 = 400, 30 x 30 = 900, 40 x 30 = 1.200, 50 x 20 = 1.000, 60 x 10 = 600.

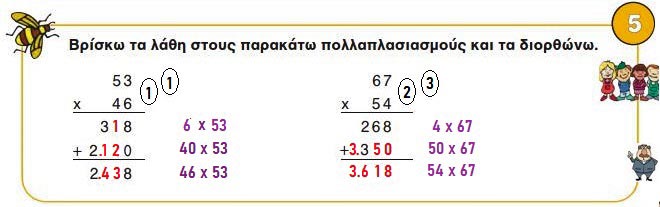
5. Βρίσκω τα λάθη στους παρακάτω πολλαπλασιασμούς και τα διορθώνω.
☛ 46 x 53 = (40 + 6) x 53 = (6 x 53) + (40 x 53) = 318 + 2.120 = 2.438

☛ 54 x 67 = (50 + 4) x 67 = (4 x 67) + (50 x 67) = 268 + 3.350 = 3.618

6. Κάνε αυτούς τους πολλαπλασιασμούς. Τι παρατηρείς;
☛ 3 x 74 = 222  ☛ 60 x 74 = 4.440
☛ 63 x 74 = (60 + 3) x 74 = (3 x 74) + (60 x 74) = 222 + 4.440 = 4.662
☛ 36 x 74 = (30 + 6) x 74 = (6 x 74) + (30 x 74) = 440 + 2.220 = 2.664

Παρατηρούμε ότι το πρώτο μερικό γινόμενο του γ' πολλαπλασιασμού, είναι το ίδιο με το γινόμενο του α', και το δεύτερο μερικό γινόμενο, είναι το ίδιο με το γινόμενο του β'. Επίσης, το πρώτο μερικό γινόμενο του δ' πολλαπλασιασμού, είναι το γινόμενο του β' διαιρεμένο δια 10 και το δεύτερο μερικό γινόμενο, είναι το γινόμενο του α' πολλαπλασιασμένο επί 10. Ακόμα στους πολλαπλασιασμούς γ' και δ', τα ολικά γινόμενά τους, αποτελούνται από τα ίδια ψηφία, γραμμένα αντίστροφα.

7.1 Γράφω με μορφή γινομένου πόσες καραμέλες έχει η μια καρτέλα.
☛ Αφού η καρτέλα έχει 4 σειρές καραμέλες και κάθε σειρά έχει από 9, τότε όλες μαζί είναι: 4 x 9 = 36 καραμέλες.

7.2 Πόσες καραμέλες έχει μέσα το κουτί;
☛ Αφού το κουτί έχει 24 καρτέλες και κάθε καρτέλα έχει 36 καραμέλες, τότε όλες μαζί είναι: 24 x 36 = 864 καραμέλες.