Κεφ. 32ο: Επαναληπτικό μάθημα - Μαθηματικά Γ' Δημοτικού

Το κεφάλαιο 32 είναι το πέμπτο επαναληπτικό των μαθηματικών της Γ' Δημοτικού και σε αυτό έχουμε να λύσουμε τις παρακάτω ασκήσεις στο βιβλίο και το τετράδιο εργασιών. Ας δούμε πώς θα τις λύσουμε.

1. Γράφω και αναλύω τους αριθμούς..
☛ 1972 = 1Χ 9Ε 7Δ 2Μ , 1689 = 1Χ 6Ε 8Δ 9Μ , 2132 = 2Χ 1Ε 3Δ 2Μ ,  2463 = 2Χ 4Ε 6Δ 3Μ , 3020 = 3Χ 0Ε 2Δ 0Μ ,  3984 = 3Χ 9Ε 8Δ 4Μ ,  

2. Στις 29 Μαρτίου του 1896, ο Σπύρος Λούης τερμάτισε πρώτος στον Μαραθώνιο Δρόμο των πρώτων σύγχρονων Ολυμπιακών Αγώνων που έγιναν στην Αθήνα. Πόσα χρόνια έχουν περάσει από τότε μέχρι σήμερα;
☛ Λύση: Σήμερα έχουμε 2020, οπότε από το 1896 μέχρι σήμερα έχουν περάσει: 2020 - 1896 = 124 χρόνια.
* Προσοχή, η απάντηση εξαρτάται από τη χρονιά που βρισκόμαστε.

3. Βρίσκω τους αριθμούς Α και Β.
☛ Αριθμός Α: 1 χιλιάδα 13 εκατοντάδες 15 δεκάδες 28 μονάδες = (1 x 1.000) + (13 x 100) + (15 x 10) + (28 x 1) = 1.000 + 1.300 + 150 + 28 = 2.478

☛ Αριθμός B: 1 χιλιάδα 16 εκατοντάδες 23 δεκάδες 32 μονάδες = (1 x 1.000) + (16 x 100) + (23 x 10) + (32 x 1) = 1.000 + 1.600 + 230 + 32 = 2.862

4. Βρίσκω τις πράξεις και γράφω το αποτέλεσμα.
☛ 2.500 + 400 = 2.900, 2.635 - 600 = 2.035, 1.550 + 300 = 1.850, 2.858 - 1.850 = 1.008, 1.111 + 1.111 = 2.222, 3.000 - 1.450 = 1.550

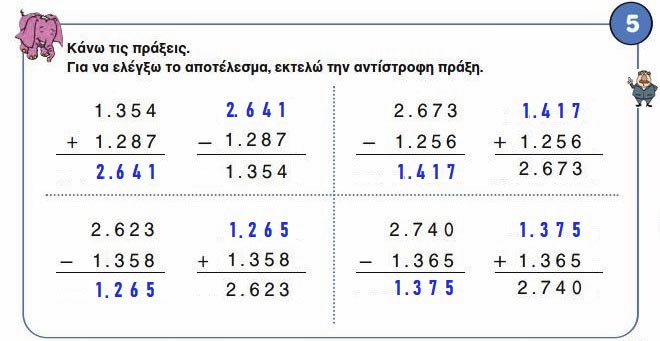
5. Κάνω τις πράξεις. Για να ελέγξω το αποτέλεσμα, εκτελώ την αντίστροφη πράξη.
☛ 1.354 + 1.287 = 2.641 ⇒ 2.641 - 1.287 = 1.354
☛ 2.623 ― 1.358 = 1.265 ⇒ 1.265 + 1.358 = 2.623

☛ 2.673 ― 1.256 = 1.417 ⇒ 1.417 + 1.256 = 2.673
☛ 2.740 ― 1.365 = 1.375 ⇒ 1.375 + 1.365 = 2.740

6.1 Πόσα μήλα έχει το ένα τελάρο;
☛ Το τελάρο έχει 3 σειρές μήλα και η κάθε σειρά έχει από 5 μήλα.
Το γράφω με μορφή γινομένου: 3 x 5 = 15 μήλα.

6.2 Πόσα μήλα έχουν τα 6 τελάρα;
☛ Το 1 τελάρο έχει 15 μήλα, άρα τα 6 έχουν: 6 x 15 = 90 μήλα.

6.3 Πόσα μήλα έχουν τα 28 τελάρα;
☛ Το 1 τελάρο έχει 15 μήλα, άρα τα 28 έχουν: 15 x 28 = (10 + 5) x (20 + 8) = (5 x 8) + (5 x 20) + (10 x 8) + (10 x 20) = 40 + 100 + 80 + 200 = 420 μήλα.

6.4 Πόσα μήλα έχουν τα 100 τελάρα;
☛ Το 1 τελάρο έχει 15 μήλα, άρα τα 100 έχουν: 15 x 100 = 1.500 μήλα.

Κεφ. 32ο: Επαναληπτικό μάθημα - Τετράδιο Εργασιών - Λύσεις Ασκήσεων

1. Υπολογίζω και γράφω τα γινόμενα.

18 x 8 = 144,  23 x 4 = 92, 35 x 5 = 175, 44 x 7 = 308, 56 x 3 = 168, 61 x 5 = 305.

2. Συμπληρώνω τα κενά με αριθμούς ή αριθμολέξεις.
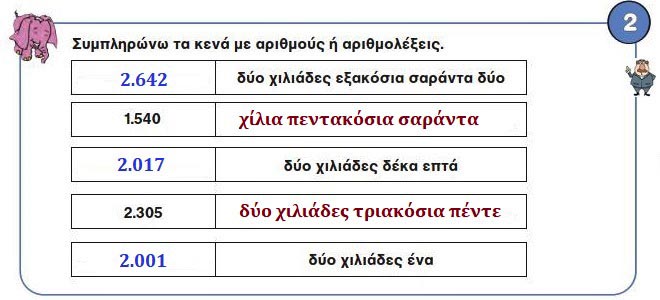
☛ 2.642  ⇒ δύο χιλιάδες εξακόσια σαράντα δύο
☛ 1.540  ⇒ χίλια πεντακόσια σαράντα
☛ 2.017  ⇒ δύο χιλιάδες δέκα επτά
☛ 2.305  ⇒ δύο χιλιάδες τριακόσια πέντε
☛ 2.001  ⇒ δύο χιλιάδες ένα

3.1 Υπολογίζω το γινόμενο 23 x 17. Επιβεβαιώνω το αποτέλεσμα με την αριθμομηχανή.
☛ 17 x 23 = (10 + 7) x (20 + 3) = (7 x 3) + (7 x 20) + (10 x 3) + (10 x 20) = 21 + 140 + 30 + 200 = 391 μήλα.

3.2 Χρησιμοποιώ το αποτέλεσμα του προηγούμενου πολλαπλασιασμού, για να υπολογίσω τα παρακάτω γινόμενα. Υπολογίζω τα γινόμενα αυτά, χωρίς να κάνω πολλαπλασιασμό και χωρίς αριθμομηχανή.
23 x 18   24 x 17   23 x 170

☛ 23 x 18 = (23 x 17) + (23 x 1) = 391 + 23 = 414
☛ 24 x 17 = (23 x 17) + (1 x 17) = 391 + 17 = 408
☛ 23 x 170 = (23 x 17) x 10 = 391 x 10 = 3.910

Επιβεβαιώνω το αποτέλεσμα με την αριθμομηχανή.

4. Υπολογίζω και γράφω τα γινόμενα.
☛ 14 x 20 = 280, 21 x 30 = 630, 34 x 20 = 680, 18 x 30 = 540, 12 x 40 = 480, 15 x 50 = 750.

5. Κάνω τους παρακάτω πολλαπλασιασμούς.
54 x 35 = (4 x 35) + (50 x 35) = 140 + 1.750 = 1.890
68 x 43 = (8 x 43) + (60 x 43) = 344 + 2.580 = 2.924
87 x 40 = (7 x 40) + (80 x 40) = 280 + 3.200 = 3.480
89 x 76 = (9 x 76) + (80 x 76) = 684 + 6.080 = 6.764

6. Βουνά της Ελλάδας
6.1 Ποια είναι τα δύο ψηλότερα βουνά στον διπλανό πίνακα;
☛ Τα δύο ψηλότερα βουνά είναι ο Όλυμπος (2.917) και ο Σμόλικας (2.637).

Τι διαφορά ύψους έχουν μεταξύ τους τα δύο αυτά βουνά;
☛ Έχουν: 2.917 - 2.637 = 280 μέτρα διαφορά και ψηλότερος είναι ο Όλυμπος.

6.2 Πόσο πιο ψηλός είναι ο Όλυμπος από τον Βόρα;
☛ Είναι: 2.917 - 2.524 = 393 μέτρα ψηλότερος.