Κεφ. 25ο: Ισοδύναμα κλάσματα - Μαθηματικά Γ' Δημοτικού

Στο εικοστό πέμπτο κεφάλαιο των μαθηματικών της Γ' Δημοτικού, θα μάθουμε για την βασική ιδιότητα των κλασμάτων που είναι η ισοδυναμία. Μέσα από καταστάσεις της καθημερινής ζωής, όπως ο χωρισμός συνεχών μεγεθών (π.χ. πίτσες και σοκολάτες) και διακριτών μεγεθών (π.χ. τα νομίσματα), θα μάθουμε ότι κάποιες ποσότητες μπορούμε να τις αποδίδουμε με δύο, τρία ή και περισσότερα κλάσματα. Π.χ.: Μισή πίτσα ή μισό ευρό, που μπορούμε να τα συμβολίσουμε με τα κλάσματα: 1/2, 2/4, 4/8, 8/16, 16/32, 50/100 κλπ.

Πάμε να δούμε ποιες εργασίες και ασκήσεις έχει το βιβλίο μαθητή και το τετράδιο εργασιών, και πώς θα τις λύσουμε.

1. Τα κομμάτια της πίτσας. Οι τρεις ίδιες πίτσες είναι κομμένες με διαφορετικό τρόπο. Από κάθε πίτσα θέλουμε να πάρουμε τη μισή.

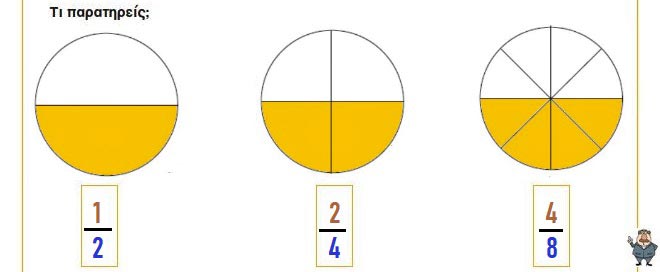
Χρωμάτισε σε κάθε πίτσα τη μισή και γράψε κάτω από την κάθε μία, με κλάσμα, το μέρος που είναι χρωματισμένο.
☛ Η πρώτη πίτσα είναι κομμένη σε δύο κομμάτια, οπότε ζωγραφίζουμε το ένα, που είναι το μισό της.
☛ Η δεύτερη πίτσα είναι κομμένη σε τέσσερα κομμάτια, οπότε ζωγραφίζουμε τα δύο, που είναι το μισό της.
☛ Η τρίτη πίτσα είναι κομμένη σε οχτώ κομμάτια, οπότε ζωγραφίζουμε τα τέσσερα, που είναι το μισό της.
Δηλαδή το μισό στην πρώτη πίτσα είναι το 1/2, στη δεύτερη τα 2/4 και στην τρίτη τα 4/8. Τα κλάσματα αυτά, αν και διαφορετικά μεταξύ τους, συμβολίζουν την ίδια αξία, είναι ίσα μεταξύ τους και ονομάζονται ισοδύναμα.

Δείτε επίσης: Εισαγωγή στα κλάσματα

• Μπορείς να γράψεις το κλάσμα με διαφορετικούς τρόπους;
☛ Το μισό της πρώτης πίτσας είναι: 1/2, το μισό της δεύτερης: 2/4 και το 1/2, και το μισό της τρίτης: 4/8 και 1/2 και 2/4.

2. Τα παιδιά έχουν από μια ίδια σοκολάτα και έφαγαν:
☛ Η Άννα: Το ένα από τα δυο κομμάτια, δηλαδή το 1/2 της σοκολάτας.
☛ Ο Γιώργος: Τα δύο από τα τέσσερα κομμάτια, δηλαδή τα 2/4 ή το 1/2 της σοκολάτας.
☛ Η Δανάη: Το ένα από τα τρία κομμάτια, δηλαδή το 1/3 της σοκολάτας.
☛ Ο Θωμάς: Τα δύο από τα έξι κομμάτια, δηλαδή τα 2/6 ή το 1/3 της σοκολάτας.

• Ποια παιδιά έφαγαν την ίδια ποσότητα σοκολάτας;
☛ Την ίδια ποσότητα σοκολάτας έφαγαν η Άννα με το Γιώργο, που έφαγαν τη μισή και η Δανάη με το Θωμά, που έφαγαν το ένα τρίτο.

• Ποια κλάσματα έχουν την ίδια αξία;
☛ Την ίδια αξία έχουν τα κλάσματα: 1/2 = 2/4 και 1/3 = 2/6.

3. Σχηματίζω ένα ευρώ με διαφορετικούς τρόπους και βρίσκω ισοδύναμα κλάσματα.
☛ Το 50λεπτο τι μέρος του ενός ευρώ είναι; 👉 Το 50λεπτο είναι το 1/2 του ενός ευρώ και είναι ίσο με 5/10 και 50/100 του ευρώ.
☛ Τα πέντε 10λεπτα τι μέρος του ενός ευρώ είναι; 👉 Τα πέντε 10λεπτα είναι τα 5/10 του ενός ευρώ και είναι ίσα με 1/2 και με 50/100 του ευρώ.
☛ Τι παρατηρείς; 👉 Παρατηρώ ότι το ένα 50λεπτο και τα 5 δεκάλεπτα έχουν την ίδια αξία, δηλαδή μισό ευρώ.
☛ Βρίσκω ότι: 👉 1/2 = 5/10 = 50/100 είναι ίσα, αφού συμβολίζουν την ίδια αξία, δηλαδή είναι ισοδύναμα.

Κεφ. 25ο: Ισοδύναμα κλάσματα - Τετράδιο Εργασιών - Λύσεις Ασκήσεων

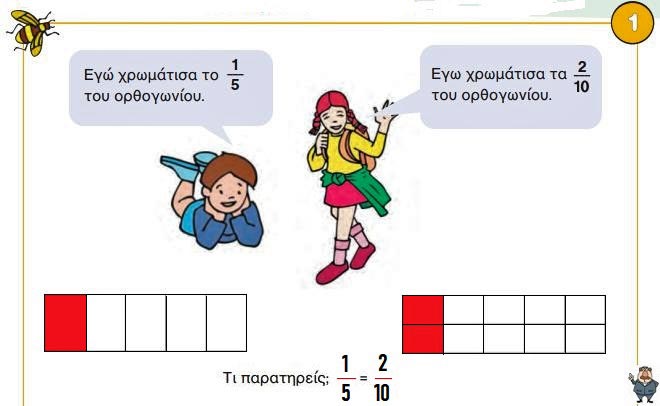
1. Το αγόρι χρωμάτισε το 1/5 του ορθογωνίου και το κορίτσι τα 2/10 του ορθογωνίου. Τι παρατηρείς;
☛ Το αγόρι και το κορίτσι ζωγράφισαν ίδιο τμήμα του ορθογωνίου, άρα το 1/5 και τα 2/10 είναι ίσα, γιατί έχουν την ίδια αξία, δηλαδή είναι ισοδύναμα.

Δείτε κι αυτό: Οι κλασματικές μονάδες

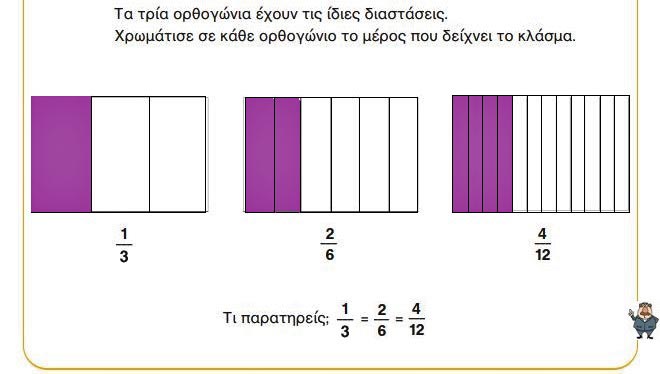
• Τα τρία ορθογώνια έχουν τις ίδιες διαστάσεις.
Χρωμάτισε σε κάθε ορθογώνιο το μέρος που δείχνει το κλάσμα.
☛ Στο πρώτο ορθογώνιο, το κλάσμα μάς δείχνει πως πρέπει να ζωγραφίσουμε το ένα από τα τρία μέρη, το 1/3.
☛ Στο δεύτερο ορθογώνιο, το κλάσμα μάς δείχνει πως πρέπει να ζωγραφίσουμε τα δύο από τα έξι μέρη, τα 2/6.
☛ Στο τρίτο ορθογώνιο, το κλάσμα μάς δείχνει πως πρέπει να ζωγραφίσουμε τα τέσσερα από τα δώδεκα μέρη, τα 4/12.

• Τι παρατηρείς;

☛ Τα κλάσματα 1/3, 2/6, 4/12, αν και διαφορετικά μεταξύ τους είναι ίσα, γιατί συμβολίζουν την ίδια αξία, το 1/3 του ορθογωνίου, δηλαδή είναι ισοδύναμα.

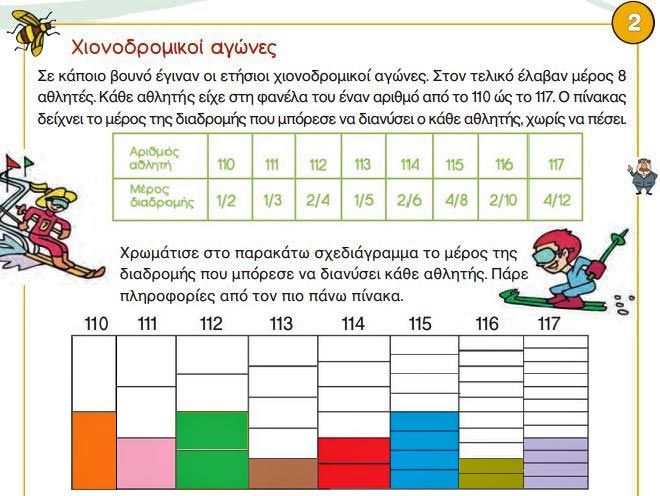
2. Χιονοδρομικοί αγώνες. Σε κάποιο βουνό έγιναν οι ετήσιοι χιονοδρομικοί αγώνες. Στον τελικό έλαβαν μέρος 8 αθλητές. Κάθε αθλητής είχε στη φανέλα του έναν αριθμό από το 110 ώς το 117. O πίνακας δείχνει το μέρος της διαδρομής που μπόρεσε να διανύσει ο κάθε αθλητής, χωρίς να πέσει.
• Χρωμάτισε στο παρακάτω σχεδιάγραμμα το μέρος της διαδρομής που μπόρεσε να διανύσει κάθε αθλητής. Πάρε πληροφορίες από τον πιο πάνω πίνακα.
☛ Ο αθλητής 110 διάνυσε το 1 από τα 2 τμήματα της διαδρομής,
☛ Ο αθλητής 111 διάνυσε το 1 από τα 3 τμήματα της διαδρομής,
☛ Ο αθλητής 112 διάνυσε τα 2 από τα 4 τμήματα ή αλλιώς το 1/2 της διαδρομής,
☛ Ο αθλητής 113 διάνυσε το 1 από τα 5 τμήματα της διαδρομής,
☛ Ο αθλητής 114 διάνυσε τα 2 από τα 6 τμήματα ή αλλιώς το 1/3 της διαδρομής,
☛ Ο αθλητής 115 διάνυσε τα 4 από τα 8 τμήματα ή αλλιώς το 1/2 της διαδρομής,
☛ Ο αθλητής 116 διάνυσε τα 2 από τα 10 τμήματα ή αλλιώς το 1/5 της διαδρομής,
☛ Ο αθλητής 117 διάνυσε τα 4 από τα 12 τμήματα ή αλλιώς το 1/3 της διαδρομής.

1. Ποιοι αθλητές διάνυσαν την ίδια απόσταση με τον αθλητή που είχε αριθμό 110;
☛ Την ίδια απόσταση με τον αθλητή που είχε αριθμό 110 διάνυσαν οι αθλητές που είχαν τους αριθμούς: 112 και 115.

2. Ποιοι αθλητές διάνυσαν απόσταση ίση με το 1/3 της διαδρομής;
Απόσταση ίση με το 1/3 της διαδρομής, διάνυσαν οι αθλητές που είχαν τους αριθμούς: 111, 114 και 117.

3. Ποιοι αθλητές διάνυσαν απόσταση ίση με το 1/5 της διαδρομής;
Απόσταση ίση με το 1/5 της διαδρομής, διάνυσαν οι αθλητές που είχαν τους αριθμούς: 113 και 116.

4. Παρατήρησε το πιο πάνω σχεδιάγραμμα και γράψε τις ισοδυναμίες κλασμάτων:
α) 1/2 = 2/4 = 4/8,  β) 1/3 = 2/6 = 4/12,   γ) 1/5 = 2/10 = 4/20.

Δείτε επίσης: Κλασματικές μονάδες & απλοί κλασματικοί αριθμοί