Στο δέκατο πέμπτο κεφάλαιο των μαθηματικών της Β' Δημοτικού, θα μάθουμε να χαράζουμε ευθύγραμμα τμήματα με προϋποθέσεις και να υπολογίζουμε το μήκος διαδοχικών ευθύγραμμων τμημάτων. Επίσης να χρησιμοποιούμε το χάρακα για να μετράμε το μήκος των πλευρών απλών γεωμετρικών σχημάτων και να συνδέουμε το όνομά τους με τον αριθμό των πλευρών ή των γωνιών τους. Π.χ. το τετράπλευρο έχει 4 γωνίες και 4 πλευρές.
Πάμε να δούμε ποιες εργασίες και ασκήσεις έχει το βιβλίο μαθητή και το τετράδιο εργασιών, και πώς θα τις λύσουμε.
Πρώτα όμως, ας κοιτάξουμε την θεωρία του μαθήματος:
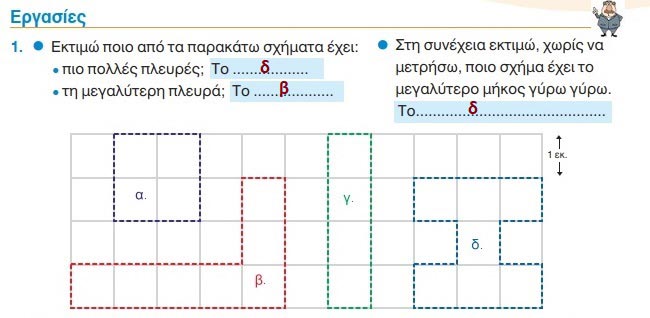
Το μεγαλύτερο μήκος (περίμετρο) το έχουν τα σχήματα β και δ, που επίσης είναι και ίσια μεταξύ τους.
Υπάρχουν δύο γεωμετρικά σχήματα με 4 πλευρές, το τετράγωνο, που έχει όλες του τις πλευρές ίσες, και το ορθογώνιο παραλληλόγραμμο, που έχει τις 2 απέναντι πλευρές του ίσες.
Αν διαλέξουμε να φτιάξουμε ένα τετράγωνο, θα πρέπει πρώτα να υπολογίσουμε τα μήκη που θα έχουν οι πλευρές του. Αφού η περίμετρος (το συνολικό μήκος των πλευρών του) είναι 20 εκατοστά, χωρίζουμε τα 20εκ. σε 4 ίσα κομμάτια, για να βρούμε το μήκος της κάθε πλευράς, δηλαδή 20εκ. = 5εκ. + 5εκ. + 5εκ. + 5εκ.
Κοιτάζοντας όμως το βιβλίο μας, βλέπουμε ότι δεν υπάρχει αρκετός χώρος για να φτιάξουμε τετράγωνο με μήκος πλευράς 5εκ., οπότε αναγκαστικά θα φτιάξουμε ένα ορθογώνιο παραλληλόγραμμο με μήκος στην κάθετη πλευρά το πολύ ως 4εκ. Έτσι προχωράμε ως εξής:
Λέμε ότι, αν η κάθετη πλευρά είναι 4εκ., τότε 4εκ. + 4εκ. = 8εκ. οι δύο κάθετες πλευρές, οπότε οι δύο οριζόντιες θα πρέπει να είναι: 20εκ. - 8εκ. = 12εκ. = 6εκ + 6 εκ. Άρα η οριζόντιες πλευρές θα είναι από 6εκ. η κάθε μία. Μπορούμε όμως να το φτιάξουμε και με άλλες διαστάσεις όπως:
3εκ. + 3εκ. = 6εκ. 20εκ. - 6εκ. = 14εκ. = 7εκ. + 7εκ. ή
2εκ. + 2εκ. = 4εκ. 20εκ. - 4εκ. = 16εκ. = 8εκ + 8 εκ. ή
1εκ. + 1εκ. = 2εκ. 20εκ. - 2εκ. = 18εκ. = 9εκ + 9 εκ.
α
Πάμε να δούμε ποιες εργασίες και ασκήσεις έχει το βιβλίο μαθητή και το τετράδιο εργασιών, και πώς θα τις λύσουμε.
Πρώτα όμως, ας κοιτάξουμε την θεωρία του μαθήματος:
Περίμετρος ονομάζεται το μήκος που έχει γύρω γύρω ένα σχήμα, και την βρίσκουμε προσθέτοντας το μήκος όλων των πλευρών του.
Αν διαλέξουμε να φτιάξουμε ένα τετράγωνο, θα πρέπει πρώτα να υπολογίσουμε τα μήκη που θα έχουν οι πλευρές του. Αφού η περίμετρος (το συνολικό μήκος των πλευρών του) είναι 20 εκατοστά, χωρίζουμε τα 20εκ. σε 4 ίσα κομμάτια, για να βρούμε το μήκος της κάθε πλευράς, δηλαδή 20εκ. = 5εκ. + 5εκ. + 5εκ. + 5εκ.
Κοιτάζοντας όμως το βιβλίο μας, βλέπουμε ότι δεν υπάρχει αρκετός χώρος για να φτιάξουμε τετράγωνο με μήκος πλευράς 5εκ., οπότε αναγκαστικά θα φτιάξουμε ένα ορθογώνιο παραλληλόγραμμο με μήκος στην κάθετη πλευρά το πολύ ως 4εκ. Έτσι προχωράμε ως εξής:
Λέμε ότι, αν η κάθετη πλευρά είναι 4εκ., τότε 4εκ. + 4εκ. = 8εκ. οι δύο κάθετες πλευρές, οπότε οι δύο οριζόντιες θα πρέπει να είναι: 20εκ. - 8εκ. = 12εκ. = 6εκ + 6 εκ. Άρα η οριζόντιες πλευρές θα είναι από 6εκ. η κάθε μία. Μπορούμε όμως να το φτιάξουμε και με άλλες διαστάσεις όπως:
3εκ. + 3εκ. = 6εκ. 20εκ. - 6εκ. = 14εκ. = 7εκ. + 7εκ. ή
2εκ. + 2εκ. = 4εκ. 20εκ. - 4εκ. = 16εκ. = 8εκ + 8 εκ. ή
1εκ. + 1εκ. = 2εκ. 20εκ. - 2εκ. = 18εκ. = 9εκ + 9 εκ.
Κεφ. 15ο: Μετρώ ευθύγραμμα τμήματα - Τετράδιο Εργασιών - Λύσεις ασκήσεων
0 Σχόλια